Basics of Acoustics

The sound pressure in air is a compressional wave. A sound wave in the free air sets in motion air particles around the positions they have at rest assuming there is no additional flow.
Where a large number of particles stand in a small volume at a given time (top plot of figure above) the sound pressure over this volume increases at this same time (bottom plot).
The differences and common points between propagative and standing waves are represented in the figure below. Three waves are displayed in the figure.
The first one, at the top, represents a wave propagating from left to right.
The second one, in the middle, represents a wave propagating from right to left.
The third one, at the bottom, represents the addition of the two previous propagating waves, point to point and time to time. Note that the zeros and extrema of this last waves stand at fixed positions contrary to the previous propagating waves. The last wave is an example of a standing wave.

Wave number
The angular, or circular, wave number 𝑘, often misleadingly abbreviated as wave number, is the modulus of the wave vector. It is inversely proportional to the wavelength λ.
The wave number is the spatial analogue of the angular frequency: application of a Fourier transformation on data in the time domain yields a frequency spectrum, applied on data in the spatial domain (data as a function of position) yields a spectrum as a function of the wave number. Note that the exact definition of the wave number depends on the physics field studied. In mechanics, the angular wavenumber is defined as:
where 𝑓 is the frequency (in Hertz), ω is the angular frequency (in rad.s⁻¹) and 𝑣𝜙 is the phase velocity of the wave (in m.s⁻¹).
Complex wave numbers
Complex wave numbers are a commonly way to account for dissipations.
For a harmonic time dependence of the form 𝑒𝑗𝜔𝑡, a pressure wave propagating toward negative 𝑥 writes:
If the wavenumber 𝑘 is a complex quantity of the form k=α+jβ with α and β defined as real positive quantities, the pressure wave can be re-written as:
e−βx is an exponential attenuation (or decay) with β as the characteristic dimension.
Complex and frequency dependent wave number
The dissipation mechanisms (e.g. visco-inertial effects, thermal effects…) can usually not be considered as constant with the frequency (see e.g. the page about the viscous boundary layer). Thus, the complex wave number is also frequency dependent (as is the velocity 𝑣𝜙).
This frequency dependence implies, at least in a given frequency range, a dispersion of the wave following Kramers-Kronig relations.
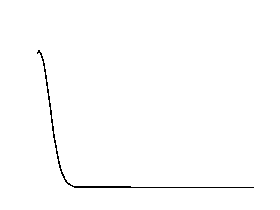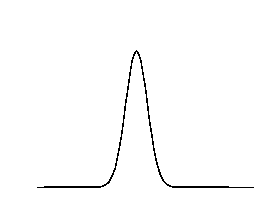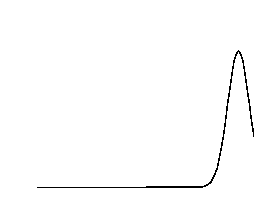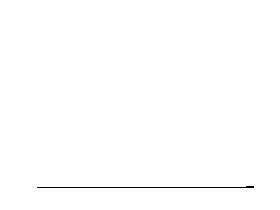
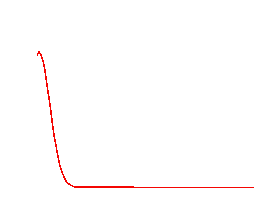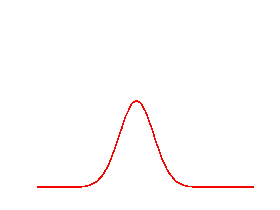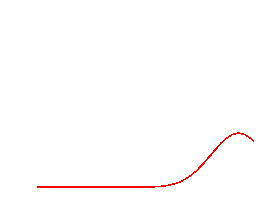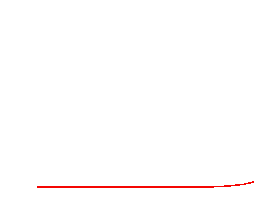
Wave dispersion
Simulations of a propagating gaussian pulse in a medium with or without dispersion. Top figure without dispersion, bottom figure with dispersion.
Helmholtz resonator
The resonance frequency of a Helmholtz resonator is computed as:
where:
- γ is the ratio of specific heats (1.4 for air),
- P₀ the atmospheric pressure in N.m⁻² (or Pa),
- ρ the mass density of air at rest (1.2 kg.m⁻³),
- Aₙ the cross section area of the resonator neck,
- for a circular cross-section of radius rₙ, Aₙ = πrₙ²,
- Lₙ the length of the resonator neck,
- V_c the volume of the resonator cavity
- for a spherical cavity of radius r_c, V_c = 4/3 × πr_c³.
Helmholtz resonator can be considered as a mass-spring system with a resonance frequency computed as:
where m is a mass and 𝑘 a stiffness.
The mass is composed of the particles inside the neck while the much larger number of particles inside the cavity constitutes the spring stiffness.
