Delany-Bazley model
在大量对孔隙率接近 1.00 的纤维材料进行的测量中,Delany 和 Bazley [DB70] 提出了这类材料的复波数 k(在 [DB70] 中为 γ/j )和特征阻抗 Zc 的经验表达式。
使用 +jωt 的时间约定,由 Delany 和 Bazley 得到的特征阻抗和波数表达式为:
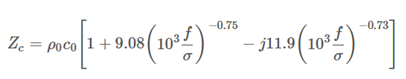
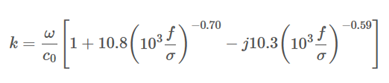
其中,ρ0 和 c0 分别为空气的密度和空气中的声速,ω=2πf 为角频率,σ 为波传播方向上的静态空气流阻(以 N.m⁻⁴.s 为单位)。
作者提出这些幂律表达式有效的边界条件为:
0.01 < f/σ < 1.00
这个经验模型在上述近似频率范围内可以提供对 k 和 Zc 的合理估计,由于其简单性仍然被广泛使用:只需要一个参数 σ 来描述材料的声学行为。
Allard 和 hampoux [AC92] 后来使用了对实验数据的先前拟合:
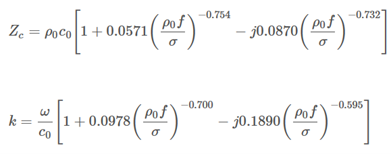
具有与上述相同边界的情况。
k 和Zc 的两种表达式给出非常接近的结果。
在多层情况下,Miki [Mik90] 注意到使用 Delany-Bazley 模型计算的表面阻抗的实部在低频时有时会变为负值,表示出非物理结果。基于 Delany 和 Bazley 的测量数据,Miki 提出了对上述表达式的修改,以纠正表面阻抗的行为。
强烈建议使用Miki报告的修订表达式来计算k和Zc。
Delany-Bazley-Miki model:
Delany-Bazley-Miki [Mik90] 模型包含了对 Delany-Bazley 模型 [DB70] 中复波数k和特征阻抗Zc的修订表达式。
在多层情况下,Miki 注意到使用原始的 Delany-Bazley 模型计算的表面阻抗的实部有时会在低频时变为负值,表示出非物理结果。基于 20 年前 Delany 和Bazley对孔隙率接近 1.00 的纤维材料进行的测量数据,Miki 建议使用以下表达式来计算波数和特征阻抗(假定使用 +a+jωt 的时间约定):
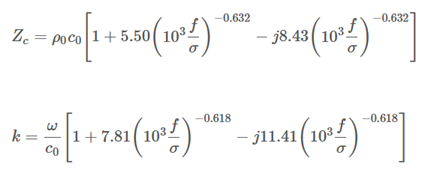
原始的 Delany-Bazley 模型和Miki对其进行修改之间的时间流逝部分解释了尽管 Miki 的修正更可取,但 Delany-Bazley 表达式仍然被广泛使用。
Delany 和 Bazley 提出的原始表达式的有效性边界为:
0.01 < f/σ < 1.00
Miki 小心翼翼地避免对这些边界进行外推,即使他观察到他的修正表达式在更大的频率范围内表现良好,特别是对于 f/σ < 0.01。
参考文献:
[DB70] Delany M. E. and Bazley E. N., Acoustical properties of fibrous absorbent materials, Applied Acoustics 3, 1970, pp. 105-116
[DB69] Delany M. E. and Bazley E. N., Acoustical characteristics of fibrous absorbent materials, Report of the National Physical Laboratory – Aerodynamics division, March 1969
[AC92] Allard J.-F. and Champoux Y., New empirical equations for sound propagation in rigid frame fibrous materials, J. Acoust. Soc. Am. 91(6), 1992, pp. 3346-3353
[Mik90] Miki Y., Acoustical properties of porous materials – Modifications of Delany-Bazley models, J. Acoust. Soc. Jpn (E). 11(1), 1990, pp. 19-24
