FFT 基础知识

快速傅里叶变换（FFT）在音频与声学测量领域扮演着至关重要的角色，能够将时间域信号转换为频率域，从而揭示信号的频率特性。FFT 技术不仅广泛应用于机械故障诊断、质量控制和状态监测等领域，还能帮助我们深入理解信号的内在频率结构。本文将深入探讨 FFT 的工作原理，并分析其参数对测量结果的具体影响。

从数学角度来看，FFT 是一种高效的算法，用于计算离散傅里叶变换（DFT）。该过程将信号在特定时间范围内的采样值分解为多个不同频率的正弦波分量，每个分量都具有独特的振幅和相位。通过这种方式，我们可以在频域中观察到信号的特征。

信号采集

在快速傅里叶变换（FFT）分析的初始阶段，我们从信号中截取一定数量的样本进行处理。这一阶段涉及到两个关键参数：

采样率（f_s）：表示每秒钟采集的样本数量。例如，44.1 kHz 表示每秒钟采集 44100 个样本。

信号长度（L）：在 FFT 分析中使用的样本数。例如，2s 的信号长度为 88200 个样本。

通过这两个参数，我们可以推导出其他几个关键的参数。

关键参数推导

带宽（f_n）

带宽，也叫尼奎斯特频率，表示 FFT 分析能够测量的最大理论频率。其计算公式为：

\[ f_{n}=\frac{f_{s}}{2} \]

例如，当采样率为 44.1 kHz 时，最大可测频率为：

\[ f_{n}=\frac{44100}{2}=22050Hz \]

理论上，FFT 能够测量到的最高频率是 22050Hz。然而，由于模拟系统中的滤波器限制，实际系统可能无法精确测量到这个频率，可能会低于理论值（例如实际可能为 20 kHz）。

频率分辨率（Δf）

频率分辨率表示 FFT 分析中频域上两个相邻采样点之间的频率间隔。计算公式为：

\[ \Delta f=\frac{f_{s}}{L} \]

信号长度L对FFT性能的影响

在实际应用中，系统通常会提供多种采样率选项。但一旦确定了块长度（L），测量周期和频率分辨率也随之确定。这将影响FFT的性能，具体表现为：

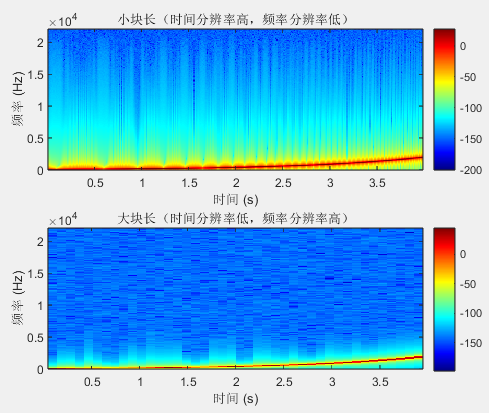
较短的块长度（L）：可以使测量周期更短，但频率分辨率较低。适用于快速响应的场景，但无法精细区分相邻的频率成分。

较长的块长度（L）：可以获得更高的频率分辨率，但测量周期会更长。适用于需要高精度频谱分析的场景，但计算量会增加。

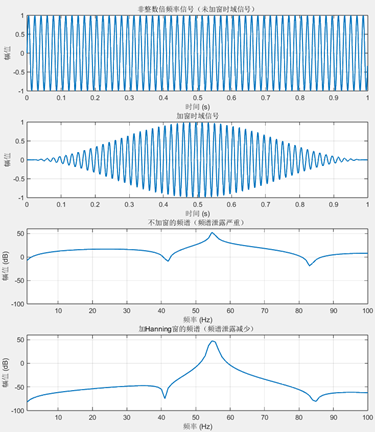
在傅里叶变换中，假设采集的信号是周期性并且无限重复的，这会导致以下两个结论：

1. FFT 仅适用于周期性信号

FFT 是基于离散傅里叶变换（DFT）的计算方法，而 DFT 假设输入信号是周期性的，即假设信号在采样的周期外是无限重复的。如果信号在采样的边界处不连续（即在信号段的开头和结尾处有不匹配），FFT 结果就会受到影响，产生频谱泄露。

2. 采样的信号段必须包含完整的一个周期

为了避免频谱泄漏，理想情况下我们希望采样的信号段包含一个完整的周期，这样可以确保信号在时间上是平滑的，在频域上不会引入不必要的误差。如果信号的周期不整除采样块长度，那么信号在一个周期内的开始和结束点就可能不匹配，从而产生时间上的不连续性，这就会导致频谱泄漏。

然而，第二个结论只有少数信号能够满足。对于频率不是频率分辨率 Δf 的整数倍的信号，如果在一个包含 L 个样本的块内进行采样，这样的信号通常会在块的开始和结束处有不同的值。这种不匹配会导致时域信号的跳变，进而引起频域上的频谱泄露（也称为弥散），即信号的能量在频谱中扩散到其他频率上。

为了避免信号的频谱泄露，实践中通常会对信号样本应用“窗口”。通过使用加权函数，信号样本的起始和结束部分会更加平滑地过渡。这样处理后，采集到的信号和后续的“加窗”信号将以幅值为零的方式开始和结束，从而避免了复杂的转换和周期性重复问题。