Johnson-Champoux-Allard (JCA) model

Johnson-Champoux-Allard 模型基于 Johnson、Koplik 和 Dashen 的研究，用于描述多孔介质内的粘滞惯性耗散效应。而 Champoux 和 Allard 的工作则用于描述热耗散效应。

粘滞惯性效应：

在 1987 年，Johnson、Koplik 和 Dashen [JKD87] 提出了一个半现象学模型，用于描述具有任意孔形的静止骨架的声学多孔材料的复密度。这个表达式是：

\[ \tilde{\rho}(\omega)=\frac{\alpha_{\infty}\rho_{0}}{\phi}\left[1+\frac{\sigma\phi}{j\omega \rho_{0}\alpha_{\infty}}\sqrt{1+j\frac{4\alpha_{\infty}^{2}\eta \rho_{0}\omega}{\sigma^{2}\Lambda^{2}\phi^{2}}} \right] \]

在计算这个动态密度时涉及到4个参数：开放孔隙率 ϕ、静态空气流阻 σ、扭曲度的高频限制 α∞ 和粘性特征长度 Λ。

正如在模型局限部分所报告的，动态质量密度表达式的实部的低频极限并不精确。

热效应：

在1991年，Champoux 和 Allard [CA91] 基于 Johnson 等人的先前工作，提出了同类多孔材料动态体积模量的表达式。

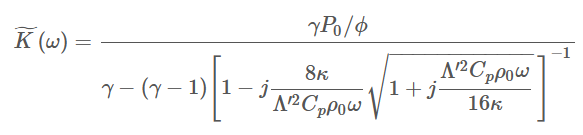
在计算这个动态体积模量时，涉及到2个参数：开放孔隙率ϕ和热特征长度Λ′。

模型局限: 错误的低频极限

由 Johnson、Koplik 和 Dashen 提供的 ρ˜ 的表达式并不能准确描述动态质量密度随着 ω 趋近零时的行为。质量密度的实部（或动态渗透率的虚部）是不正确的。同样地，由 Champoux 和 Allard 提供的 K˜ 的表达式在低频时也不正确。[我知道我需要进一步开发这一部分。请给我一些时间来完成。]Pride、Morgan 和 Gangi [PMG93] 提出了动态密度的修改表达式。然而，由 Pride、Morgan 和 Gangi 提出的表达式，经 D. Lafarge [Laf93] 进一步修改，很少被使用，因为需要对新的必要参数进行开发和表征。Pride 等人和 D. Lafarge 对 JCA 模型的修改在 Johnson-Champoux-Allard-Pride-Lafarge 模型中详细说明。

在低频情况下热效应的信息不足：

在计算 ρ˜ 并描述粘滞惯性效应时需要四个参数：低频时的 ϕ、σ=η/k0、高频和中频时的 α∞ 和 Λ。与此同时，计算 K˜ 并描述热效应时只使用了两个参数：ϕ和热特征长度 Λ′。后者用于表示热效应的中频和高频范围。

对于粘滞惯性和热效应之间的描述非对称的观察导致 Lafarge 等人 [LLAT97] 引入了一个新参数，即静态热透过率 k′0，以描述热效应的低频行为。

Lafarge 等人引入的 K˜的新模型（ρ˜保持不变）在专用页面中详细介绍了 Johnson-Champoux-Allard-Lafarge 模型。

这部分参考文献：

[JKD87] Johnson D. L., Koplik J. and Dashen R., Theory of dynamic permeability and tortuosity in fluid-saturated porous media, J. Fluid Mech. 176, 1987, pp. 379-402 ■

[CA91] Champoux Y. and Allard J.-F., Dynamic tortuosity and bulk modulus in air-saturated porous media, J. Appl. Phys. 70, 1991, pp. 1975-1979 ■

[PMG93] Pride S. R., Morgan F. D. and Gangi A. F., Drag forces of porous-medium acoustics, Phys. Rev. B 47, 1993, pp. 4964-4978 ■

[Laf93] Lafarge D., Propagation du son dans les matériaux poreux à structure rigide saturés par un fluide viscothermique (Translation: Sound propagation in rigid porous media saturated by a viscothermal fluid)., PhD thesis, Université du Maine (France), 1993 ■

[LLAT97] Lafarge D., Lemarinier P., Allard J.-F. and Tarnow V., Dynamic compressibility of air in porous structures at audible frequencies, J. Acoust. Soc. Am. 102(4), 1997, pp. 1995-2006 ■

Johnson-Champoux-Allard-Lafarge (JCAL) model：

Johnson-Champoux-Allard-Lafarge 模型基于 Johnson、Koplik 和 Dashen 的工作，用于描述多孔介质内的粘滞惯性耗散效应。Champoux 和 Allard 以及Lafarge、Lemarinier、Allard 和 Tarnow 的工作则用于描述热耗散效应。

粘滞惯性效应：

在 1987 年，Johnson、Koplik和Dashen [JKD87] 提出了一个半现象学模型，用于描述具有任意孔形的静止骨架的声学多孔材料的复密度。该表达式为：

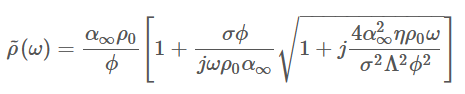
在计算这个动态密度时涉及到 4 个参数：开放孔隙率 ϕ、静态空气流阻 σ、扭曲度的高频限制 α∞ 和粘性特征长度 Λ。

正如在限制部分所报告的，动态质量密度表达式的实部的低频极限并不精确。

热效应：

在 1991 年，Champoux 和 Allard [CA91] 基于 Johnson 等人的先前工作为同类多孔材料引入了一个动态体积模量的表达式。除了上述 Johnson 等人的工作外，这项工作还导致了 Johnson-Champoux-Allard 模型的定义。

然后，由 Champoux 和 Allard 给出的 K˜ 的表达式在 1993 年被 Lafarge 等人 [LLAT97] 修改，他们强调了在低频情况下热效应缺乏信息。

事实上，从 Johnson 等人的工作计算ρ˜并描述粘滞惯性效应需要四个参数，而从 Champoux 和 Allard 的工作计算 K˜ 并描述热效应只需要两个参数。

这一观察结果促使 Lafarge 等人引入一个新的参数，即静态热透过率 k′0，以描述热效应的低频行为。

Lafarge 等人提出的新的 K˜模型为：

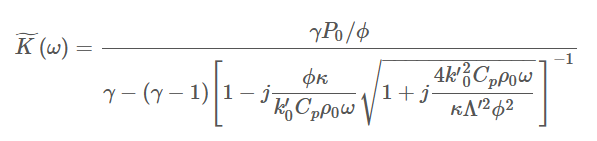
在计算这个动态体积模量时，涉及到 3 个参数：开放孔隙率 ϕ、热特征长度 Λ′ 和静态热透过率 k′0。

模型限制：

错误的低频极限

由 Johnson、Koplik 和 Dashen 提供的 ρ˜的表达式并不能准确描述动态质量密度随着 ω 趋近零时的行为。质量密度的实部（或动态渗透率的虚部）是不正确的。

同样地，由 Champoux 和 Allard 提供的 K˜ 的表达式，经 Lafarge 等人进一步修改，也在低频时不正确。[我知道我需要进一步开发这一部分。请给我一些时间来完成。]

Pride、Morgan 和 Gangi [PMG93] 提出了动态密度的修改表达式。然而，由 Pride、Morgan 和 Gangi 提出的表达式，经 D. Lafarge [Laf93] 进一步修改，很少被使用，因为需要对新的必要参数进行开发和表征。

Pride 等人和 D. Lafarge 对 JCA 模型的修改在 Johnson-Champoux-Allard-Pride-Lafarge 模型中详细说明。

这部分参考文献：

[JKD87] Johnson D. L., Koplik J. and Dashen R., Theory of dynamic permeability and tortuosity in fluid-saturated porous media, J. Fluid Mech. 176, 1987, pp. 379-402 ■

[CA91] Champoux Y. and Allard J.-F., Dynamic tortuosity and bulk modulus in air-saturated porous media, J. Appl. Phys. 70, 1991, pp. 1975-1979 ■

[LLAT97] Lafarge D., Lemarinier P., Allard J.-F. and Tarnow V., Dynamic compressibility of air in porous structures at audible frequencies, J. Acoust. Soc. Am. 102(4), 1997, pp. 1995-2006 ■

[PMG93] Pride S. R., Morgan F. D. and Gangi A. F., Drag forces of porous-medium acoustics, Phys. Rev. B 47, 1993, pp. 4964-4978 ■

[Laf93] Lafarge D., Propagation du son dans les matériaux poreux à structure rigide saturés par un fluide viscothermique (Translation: Sound propagation in rigid porous media saturated by a viscothermal fluid)., PhD thesis, Université du Maine (France), 1993 ■

Johnson-Champoux-Allard-Pride-Lafarge (JCAPL) model：

Johnson-Champoux-Allard-Pride-Lafarge (JCAPL) 模型基于 Johnson、Koplik 和 Dashen 以及 Pride、Morgan 和 Gangi 的工作，用于描述多孔介质内的粘滞惯性耗散效应。而 Champoux 和 Allard；Pride、Morgan 和 Gangi 以及 Lafarge、Lemarinier、Allard 和 Tarnow 的工作则用于描述热耗散效应。

粘滞惯性效应：

在1987年，Johnson、Koplik 和 Dashen [JKD87] 提出了一个半现象学模型，用于描述具有任意孔形的静止骨架的声学多孔材料的复密度。

该模型在 1993 年由 Pride、Morgan 和 Gangi [PMG93]（并由D. Lafarge修正）进一步完善，以考虑可能存在收缩的孔隙之间的情况。最终得到的ρ˜的表达式为：

\[ \tilde{\rho}=\frac{\rho_{0}\tilde{\alpha}(\omega)}{\phi} \] \[ \tilde{\alpha}(\omega)=\alpha_{\infty}\left[ 1+\frac{1}{j\bar{\omega}}\tilde{F}(\omega) \right] \] \[ \tilde{F}(\omega)=1-P+P\sqrt{1+\frac{M}{2P^{2}}j\bar{\omega}} \] \[ \tilde{\omega}=\frac{\omega \rho_{0}k_{0}\alpha_{\infty}}{\eta\phi} \] \[ M=\frac{8K_{0}\alpha_{\infty}}{\phi \Lambda^{2}} \] \[ P=\frac{M}{4(\frac{\alpha_{0}}{\alpha_{\infty}}-1)} \]

在计算这个动态密度时，涉及到 5 个参数：静态空气流阻 σ（或静态粘性透过率k0=η/σ）、开放孔隙率 ϕ、扭曲度的高频限制 α∞、粘性特征长度 Λ 和静态粘性扭曲度 α0。

热效应：

在1991年，Champoux 和 Allard [CA91] 根据 Johnson 等人的先前工作引入了一个动态体积模量的表达式。这个模型在 1993 年由 Pride、Morgan 和 Gangi [PMG93] 进一步完善（并由D. Lafarge修正），以考虑可能存在收缩的孔隙之间的情况。最后，在[LLAT97]的工作之后（引入了一个新参数以描述低频时的热行为：静态热透过率k′0），得到的K˜的最终表达式为：

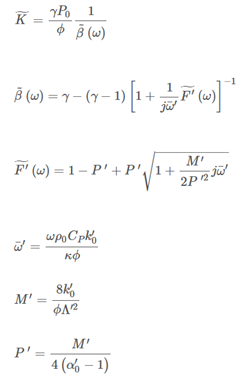
在计算这个动态体积模量时，涉及到 4 个参数：开放孔隙率 ϕ、热特征长度 Λ′、静态热透过率 k′0和静态热扭曲度 α′0。

JCA 模型和 JCAL 模型的关联：

Johnson-Champoux-Allard（JCA）和Johnson-Champoux-Allard-Lafarge（JCAL）模型可通过在上述报告的ρ˜和K˜的表达式中分别设置 M′=P=P ′=1 和 P=P ′=1来从 JCAPL 模型中恢复。

这部分参考文献：

[JKD87] Johnson D. L., Koplik J. and Dashen R., Theory of dynamic permeability and tortuosity in fluid-saturated porous media, J. Fluid Mech. 176, 1987, pp. 379-402 ■

[PMG93] Pride S. R., Morgan F. D. and Gangi A. F., Drag forces of porous-medium acoustics, Phys. Rev. B 47, 1993, pp. 4964-4978 ■

[Laf93] Lafarge D., Propagation du son dans les matériaux poreux à structure rigide saturés par un fluide viscothermique (Translation: Sound propagation in rigid porous media saturated by a viscothermal fluid)., PhD thesis, Université du Maine (France), 1993 ■

[CA91] Champoux Y. and Allard J.-F., Dynamic tortuosity and bulk modulus in air-saturated porous media, J. Appl. Phys. 70, 1991, pp. 1975-1979 ■

[LLAT97] Lafarge D., Lemarinier P., Allard J.-F. and Tarnow V., Dynamic compressibility of air in porous structures at audible frequencies, J. Acoust. Soc. Am. 102(4), 1997, pp. 1995-2006 ■

参考APMR网站