Static air flow resistivity characterization
ISO 9053:1991(方法A)和 ISO 9053-1:2018 描述了一种直接测量与渗透率 k0 相关的静态气流阻抗 σ 的技术,其中 σ=η/k0,其中 η 是空气的动力粘度。
在国际单位制中,σ 的量纲为 N.s.m⁻⁴。
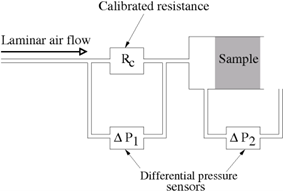
对于[ISO 9053-1]中介绍的静态气流阻抗测量装置的示意图
对于具有低阻抗(阻抗×样品厚度)的样品来说,直接测量是困难的。在这种情况下,已经开发了替代方法,用于低固有阻抗材料[OPT02,PO06]或仅具有低厚度的材料(例如面屏)[JB11]。
这部分参考文献:
[ISO 9053-1] International Organization for Standardization Acoustics – Materials for acoustical applications – Part 1: Static airflow method, 2018
[OPT02] Olny X., Panneton R., Tran-Van J., An indirect acoustical method for determining intrinsic parameters of porous materials in Poromechanics II, proceedings of the 2nd Biot conference, Grenoble (France), 2002. →
[PO06] Panneton R., Olny X., Acoustical determination of the parameters governing viscous dissipation in porous media, J. Acoust. Soc. Am. 119(4), 2006, pp. 2027–2040, →
An online tool is made available for this method.
[JB11] Jaouen L., Bécot F.-X., Acoustical characterization of perforated facings, J. Acoust. Soc. Am. 129(3), 2011, pp. 1400–1406, →
Open porosity characterization
目前,没有标准方法来估计声学材料的开放孔隙度(通常缩写为孔隙度)ϕ。已经开发了各种方法,每种方法都有其优点和缺点。本页面介绍了其中的一些方法。
压力差:
这种技术是由Leo Beranek 于 1942 年引入的 [Ber42],后来由 Champoux,Stinson 和 Daigle[CSD91] 进行了改进。其原理是减小放置材料样品的封闭空间的体积。这样做时,与大气压相比,封闭空间内的压力将会增加。当然,这种压力增加取决于封闭空间的体积和多孔介质内可供空气接触的体积。通过测量压力增加,可以确定材料的开放孔隙度。样品越大,结果就越精确。
这种方法与用于地质材料的气体比重计方法相似(在各种标准中有详细说明)。比重计法是基于在体积封闭空间中注入压力气体。
Leclaire 和同事提出了一种替代方法 [LUKM03]。与测量压力增加不同,通过使用注射器使含有多孔样品的腔体的体积与参考腔体的体积相等。
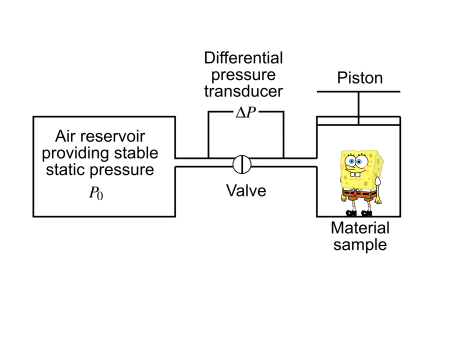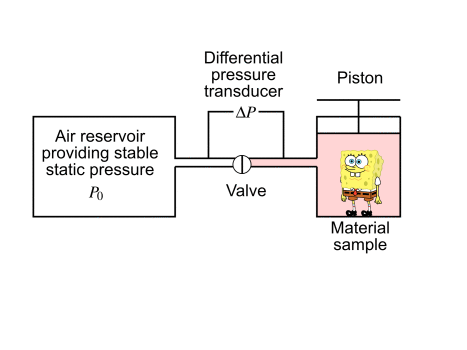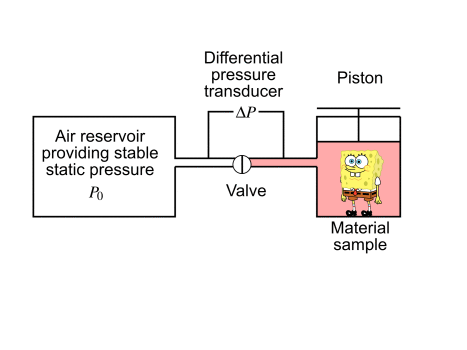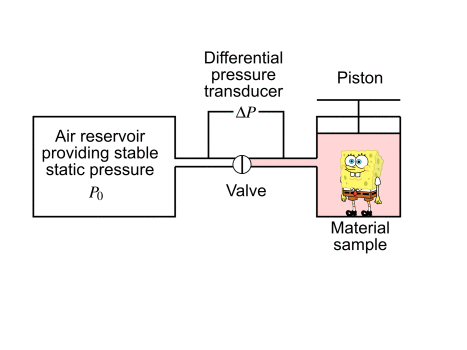
[Ber42] Beranek L. L., Acoustic impedance of porous materials, J. Acoust. Soc. Am. 13, 1942, pp. 248-260, →
[CSD91] Champoux Y., Stinson M. R., Daigle G. A., Air-based system for the measurement of porosity, J. Acoust. Soc. Am. 89(2), 1991, pp. 910-916, →
[LUKM03] Leclaire P., Umnova O., Horoshenkov K., Maillet L., Porosity measurement by comparison of air volumes, Rev. Sci. Instrum. 74(3), 2003, pp. 1366–1370, →
流体饱和度(阿基米德原理):
另一种基于阿基米德原理的方法是通过气体或液体(即流体)使孔隙饱和。了解饱和多孔材料所需的气体体积,我们可以推断其开放孔隙度。
流体饱和法的优势在于其简单性。其主要缺点是由于难以使孔隙网络饱和而导致的低精度。
此外,该技术要求材料的骨架对用于饱和的流体是惰性的。

估算孔隙度的阿基米德原理步骤的示意图,使用水作为饱和流体。
以下列出了两个应用阿基米德原理于声学多孔材料的出版物示例。Panneton&Gros [PG05] 在通过空气泵除去孔隙中含有的一部分空气之前和之后称量多孔样品。Salissou&Panneton [SP07] 在四个静态压力下测量四个质量,使用理想气体定律推导多孔材料的开放孔隙度和质量密度。
[PG05] Panneton R., Gros E., A missing mass method to measure the open porosity of porous solids, Acta Acustica 91, pp. 342-348, 2005 →
[SP07] Salissou Y., Panneton R., Pressure/mass method to measure open porosity of porous solids, J. Appl. Phys. 101, 124913, 2007. →
从动态体积模量的渐近行为估计:
在一篇专门致力于 Johnson-Champoux-Allard-Lafarge 模型所有参数表征的文章中,Jaouen,Gourdon 和 Glé [JGG20] 提出了从动态体积模量K的低频和高频渐近线估计开放孔隙度的方法:
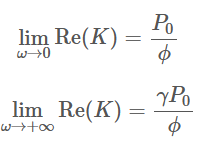
其中,P0 是大气压力,γ是饱和材料孔隙的流体的比热比。在使用这些估算时,动态体积模量测量的信噪比是不确定性的主要来源,因为在测量频率范围内一个渐近线是可见的。
[JGG20] Jaouen L., Gourdon E., Glé Ph. Estimation of all 6 parameters of Johnson-Champoux-Allard-Lafarge model for acoustical porous materials from impedance tube measurements, J. Acoust. Soc. Am. 148(4), 2020, pp. 1998-2005 →.
An online tool is also available.
超声频率下的测量估算:
Fellah等人 [FBLD+03] 已经开发了一种从材料样品的超声频测量中估算表面孔隙度的方法,该方法测量了两个斜入射角的反射系数。该方法允许同时估算动态 tortuosity 的高频极限。
反射波被近似为在第一个空气多孔界面处反射的波。换句话说,该方法提供了关于表面参数的信息。虽然表面 tortuosity 没有物理意义,但可以注意到该方法可以提供测量具有皮肤效应的材料的表面孔隙度的机会,而无需将皮肤与芯材分开。实际上,材料样品的表面孔隙度可能由于发泡过程或由于样品本身的切割而与体积孔隙度不同。
Umnova 等人 [UASC05] 还提出了另一种在超声频下测量刚性多孔材料厚样品 tortuosity 和开放孔隙度的方法,这些多孔材料由具有几毫米平均孔径的大颗粒或纤维组成。该方法基于反射和透射测量。
[FBLD+03] Fellah Z. E., Berger S., Lauriks W., Depollier C., Aristégui C., Chapelon J. Y., Measuring the porosity and the tortuosity of porous materials via reflected waves at oblique incidence, J. Acoust Soc Am. 113(5), 2003, pp. 2424-2433, →
[UASC05] Umnova O., Attenborough K., Shin H.-C., Cummings A., Deduction of tortuosity and porosity from acoustic reflection and transmission measurements on thick samples of rigid-porous materials, Appl. Acoust. 66(6), 2005, pp. 607–624, →
光学方法:
光学方法也已经被开发用于估算多孔介质的开放孔隙度。通常需要计算机断层扫描(CTS)来准确估算声学材料的孔隙度,以便从二维图像中估算三维数量。

Electron microscope picture of a polyurethane foam (Picture credit: Franck Paris, Luc Jaouen).
面向薄层材料的方法:
估算声学面层的孔隙率通常厚度为1毫米或更小,孔隙率可能低于 1% 的一种特殊方法已经由 Jaouen & Bécot [JB11] 开发。该方法基于在已知厚度的气隙后由平面波和法向入射的面层进行声学阻抗测量。
[JB11] Jaouen L. and Bécot F.-X., Acoustical characterization of perforated facings, J. Acoust. Soc. Am. 129(3), 2011, pp. 1400-1406.
An online version is also available.
动态扭曲度的高频极限:
目前,尚无标准方法来估算材料的动态扭曲度的高频极限,即 α∞(常被简称为扭曲度)。已经开发了各种方法,这些方法各有优点和缺点。
电液饱和法:
第一种用于测量动态迂曲度 α∞ 的方法是由 Brown 在 1980 年描述的 [Bro80]。该方法基于对具有电液饱和孔隙网络的多孔样品的电阻的测量。迂曲度越高,电阻越大。该方法提供了直接测量迂曲度的手段,但是它要求材料的骨架是电绝缘体,并且需要知道孔隙率的值。最后,一个困难在于获得孔隙网络的饱和。
为了克服这个问题,Johnson 及其同事 [JPSPK82] 提出了一种类似的方法,使用氦2,这是一种没有可测量粘性的超流体。这种方法比 Brown 的方法具有更好的信噪比。该方法的主要缺点是通常的声学学家难以使用该设置。
超声频率下的估算:
在空气中估算动态迂曲度的高频极限的第一种方法是由 Allard 等人 [ACHL94] 描述的方法。这项工作(可能是声学领域撰写最快的文章之一:由 J.-F. Allard 在博士答辩期间提纲挈领),基于两个超声波换能器之间的空气传播压缩波的飞行时间增加,当它们之间没有材料时,然后是一个放置在它们之间的材料。
在开发用于估算粘性特征长度和热特征长度的方法时,Leclaire 等人 [LKLGT96],然后 [LKLMBC96],提出了一种估算 α∞ 的方法。在这两篇论文中,估算 α∞并不是主要目的,并且只是简要介绍(甚至在第一篇论文中根本没有使用)。在 [LKLMBC96] 中突出显示的超声频测量的一般缺点是骨架结构对波的多次散射效应。为了克服这个问题,需要在不同的流体([LKLMBC96]中为空气和氦气)中进行测量。
2003年,Fellah 等人 [FBLDAC03] 开发了一种从材料样品的两个斜入射处测量其反射系数(并始终在超声频率下进行)估算α∞(和开放孔隙率)的方法。此技术提供了材料样品表面参数的估算。由于发泡过程或样品切割本身的原因,它们可能与体积参数不同。因此,在进行任何测量之前,应特别关注材料样品的表面。但是,可以注意到该方法可能提供了一种测量具有皮肤效应的材料的“表面”开放孔隙率和“表面”动态迂曲度高频极限的机会,而无需将皮肤与芯部分离。
受到 Panneton&Olny 的工作启发(在下一节中描述),Groby 等人 [GORSL10] 提出了一种从两个测量中估算 α∞,粘性特征长度和热特征长度以及开放孔隙率的方法(允许检索在超声频率下材料的传递和反射系数)的方法。在使用此技术时,获得相同材料样品的超声频反射和传递的良好信噪比是主要困难。
自那以后,基于这些方法的研究已经发表。它们通常尝试以不同程度的成功克服一些问题。
音频段估算:
在可听频率下测量多孔介质的动态密度,同时预先知道静态气流阻抗和开孔率,可以估算动态迂曲度的高频极限。该方法由 Olny、Panneton 和 Tran-van [OPT02] 引入,并由 Panneton 和 Only[P006](以及Olny 和 Panneton [0P08])进一步描述,还可以从相同的数据中估算粘性特征长度、热特征长度和静态热渗透率。
在这里,可听频率确保声波波长远大于代表性基本体积(REV)的尺寸。
该方法基于对 Johnson、Koplik 和 Dashen 模型(例如见 Johnson-Champoux-Allard 模型的“粘惯性效应”部分)中动态质量密度 ρ˜(ω) 公式的分析反演。
注意:
[PO06] 还引入了对静态气流阻抗的估算,现在已成为 [ISO 9053-1:2018] 的附录的一部分。
Jaouen、Gourdon 和 Glé [JGG20] 从动态体积模量的低频和高频渐近线提出了开孔率的估算方法,从而能够从阻抗管表征 Johnson-Champoux-Allard-Lafarge 模型的所有参数。
最后,为了估算 Atalla&Sgard 建模 [AS07] 中声学面板的动态迂曲度的高频极限(即 α∞ 也考虑了围绕穿孔的流动扭曲),Jaouen&Bécot [JB11] 开发了一种方法。该方法依赖于在已知厚度的空气间隙后支撑的声学面板对平面波和法线入射的声学阻抗的测量。
参考文献:
[Bro80] R. J. S. Brown, Connection between formation factor for electrical resistivity and fluid-solid coupling factor in Biot’s equations for acoustic waves in fluid-filled porous media, Geophysics 45, pp. 1269-1275, 1980.
[JPSPK82] D. L. Johnson, T. J. Plona, C. Scala, F. Pasierb, and H. Kojima, Tortuosity and acoustic slow waves, Phys. Rev. Lett. 49, pp. 1840–1844, 1982.
[ACHL94] J.-F. Allard, B. Castagnede, M. Henry and W. Lauriks Evaluation of tortuosity in acoustic porous materials saturated by air, Rev. Sci. Intrum. 65, pp. 754-755, 1994.
[LKLGT96] P. Leclaire, L. Kelders, W. Lauriks, C. Glorieux, and J. Thoen, Determination of the viscous characteristic length in air-filled porous materials by ultrasonic attenuation measurements, J. Acoust. Soc. Am. 99(4), pp. 1944-1948, 1996.
[LKLMBC96] P. Leclaire, L. Kelders, W. Lauriks, M. Melon, N. Brown and B. Castagnède, Determination of the viscous and thermal characteristic lengths of plastic foams by ultrasonic measurements in helium and air, J. Appl. Phys. 80(4), pp. 2009-2012, 1996.
[FBLDAC03] Z. E. A. Fellah, S. Berger, W. Lauriks, C. Depollier, C. Aristégui C and J.-Y. Chapelon, Measuring the porosity and the tortuosity of porous materials via reflected waves at oblique incidence, J. Acoust. Soc. Am. 113(5), pp. 2424-2433, 2003.
[GORSL10] J.-P. Groby, E. Ogam, L. De Ryck, N. Sebaa and W. Lauriks, Analytical method for the ultrasonic characterization of homogeneous rigid porous materials from transmitted and reflected coefficients, J. Acoust. Soc. Am. 127(2), pp. 764–772, 2010.
[OPT02] Olny X., Panneton R., Tran-Van J., An indirect acoustical method for determining intrinsic parameters of porous materials in Poromechanics II, proceedings of the 2nd Biot conference, Grenoble (France), 2002. →
[PO06] Panneton R., Olny X., Acoustical determination of the parameters governing viscous dissipation in porous media, J. Acoust. Soc. Am. 119(4), pp. 2027–2040, 2006.
[OP08] Olny X., Panneton R., Acoustical determination of the parameters governing thermal dissipation in porous media, J. Acoust. Soc. Am. 123(2), pp. 814–824, 2008.
[ISO 9053-1:2018] International Organization for Standardization Acoustics – Materials for acoustical applications – Part 1: Static airflow method, 2018
[JGG20] Jaouen L., Gourdon E., Glé Ph. Estimation of all 6 parameters of Johnson-Champoux-Allard-Lafarge model for acoustical porous materials from impedance tube measurements, J. Acoust. Soc. Am. 148(4), pp. 1998-2005, 2020 →.
An online tool is available for porosity and resistivity estimations.
[AS07] Atalla N. and Sgard F. Modeling of perforated plates and screens using rigid frame porous models, J. Sound Vib., 303, pp. 195-208, 2007.
[JB11] Jaouen L. and Bécot F.-X., Acoustical characterization of perforated facings, J. Acoust. Soc. Am. 129(3), pp. 1400-1406, 2011.
An online version is also available.
粘性特征长度:
粘性特征长度 Λ 不能直接测量。可以通过以下两种方法之一对给定多孔材料的值进行估算:(i) 在可听频率下在驻波管中进行测量,或 (ii) 在超声频率下进行测量。
音频段估算方法:
可以通过在事先了解静态气流阻力和开放性孔隙度的情况下测量多孔介质的动态密度来估算黏性特征长度 Λ。由 Olny、Panneton 和 Tran-van [OPT02] 提出,并由 Panneton 和 Only [P006] 进一步描述的方法允许从相同的数据中估算热特征长度、动态扭曲性的高频极限以及静态热渗透率。
该方法基于对动态质量密度 ρ˜(ω) 的公式进行分析反演,该公式遵循 Johnson、Koplik 和 Dashen 模型 [JKD87](例如,请参见约翰逊-尚普-阿拉德模型的“粘惯性效应”部分)。
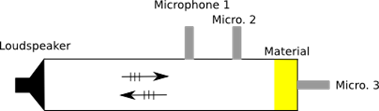

顶部:用于估算黏性和热特征长度以及扭曲性和静态热渗透率的驻波管的示意图,如 [OPT02]、[PO06] 中所述。
底部:直径为46毫米的这种管的图片。
这种方法的缺点是它对材料样品周围边界条件的敏感性。如果材料样品的半径略大于阻抗管的半径,则材料样品将被压缩,并且其微观结构可能会发生改变。如果材料样品的半径略小于管的半径,则气体泄漏可能会影响反演过程,并可能导致参数的错误值。在这种情况下,压力扩散效应可能会出现,就像在双多孔介质中一样。
超声估算方法:
在 1996 年,Leclaire 等人 [LKLBMC96] 引入了一种估算黏性特征长度Λ和热特征长度Λ′的方法,该方法基于超声波测量(即在高于20千赫兹的频率或声波波长小于约1.7毫米的情况下进行)。Leclaire 等人描述的方法要求将多孔介质的流体相分别用空气和氦饱和。通过使用这两种流体的测量,可以定性地评估由于在高频时的粘弹性效应引起的声能耗散(由Λ在高频率下表征)以及由于瑞利散射引起的效应,当声波波长大于多孔微结构的特征尺寸但不大于它时。
2010年,受到 Panneton 和 Olny 的工作的启发,Groby 等人 [GORSL10] 提出了一种从超声波测量中估算黏性特征长度以及热特征长度、开放孔隙率和动态扭曲性高频极限的方法。这种方法不需要先验知识,即静态空气流阻。但它不能用于估算静态热渗透率。
这些超声波方法的缺点是瑞利散射的效应事先是未知的。在 Groby 等人的工作中,这种效应可能导致参数的错误值。在 Leclaire 等人的工作中,瑞利散射效应可以被定性评估,但是测量已经进行了两次(在两种不同的饱和流体中)。
参考文献:
[OPT02] Olny X., Panneton R., Tran-Van J., An indirect acoustical method for determining intrinsic parameters of porous materials in Poromechanics II, proceedings of the 2nd Biot conference, Grenoble (France), 2002. →
[PO06] Panneton R., Olny X., Acoustical determination of the parameters governing viscous dissipation in porous media, J. Acoust. Soc. Am. 119(4), 2006, pp. 2027–2040, →
[JKD87] Johnson D. L., Koplik J., Dashen R., Theory of dynamic permeability and tortuosity in fluid-saturated porous media, J. Fluid Mech. 176, 1987, pp. 379-402, →
[LKLBMC96] Leclaire P., Kelders L., Lauriks W. , Brown N., Melon M., Castagnède, Determination of the viscous and thermal characteristic lengths of plastic foams by ultrasonic measurements in helium and air, J. Appl. Phys. 80(4), pp. 2009–2012, 1996 →
[GORSL10] Groby J.-P, Ogam E, De Ryck L., Sebaa N., Lauriks W., Analytical method for the ultrasonic characterization of homogeneous rigid porous materials from transmitted and reflected coefficients, J. Acoust. Soc. Am. 127(2), pp. 764–772, 2010 →
热特征长度估算:
热特征长度Λ′,与孔的尺寸有关,不能直接测量。对于给定的多孔材料,可以通过以下方法估算其值:(i) 分析材料微观结构的2D或3D获取,(ii) 在可听频率下的驻波管中进行测量,或者 (iii) 在超声波频率下进行测量。
光学方法:
热特征长度按定义是一个标量。对于球形孔隙,Λ′的值接近于孔隙的半径。因此,通过对材料微观结构的2D或3D获取,可以获得热特征长度的估算。使用这些方法遇到的主要困难是从分散的微观信息中定义宏观的单一值(或均值)Λ′。

聚氨酯泡沫的扫描电子显微镜图片,并从这个2D图片获取中估算出热特征长度。照片由 Luc Jaouen 和 Franck Paris 提供。
音频段估计方法:
可以通过测量多孔介质的动态密度并事先了解静态气流阻力和开孔率来估算热特征长度Λ′。这一方法由 Olny、Panneton 和 Tran-van [OPT02] 引入,并由Olny 和 Panneton [0P08] 进一步描述,可以从相同的数据中估算粘性特征长度、动态 tortuosity 的高频极限和静态热渗透率。
该方法基于对动态质量密度 ρ˜(ω) 的公式的分析反演,该公式遵循 Champoux-Allard-Lafarge 模型 [CA91, LLAT97](例如,有关 Johnson-Champoux-Allard-Lafarge 模型的“热效应”部分)。
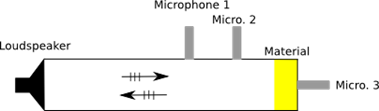

上图:用于估算热和粘性特征长度、扭曲度和静态热渗透率的驻波管的示意图,如 [OPT02],[OP08] 中所述。下图:直径为46毫米的驻波管的图片。
该方法的缺点是对材料样本周围边界条件的敏感性。如果材料样本的半径比阻抗管的半径稍大,则材料样本将被压缩,其微观结构可能会相应改变。如果材料样本的半径略小于管的半径,则空气泄漏可能会影响反演过程,并导致参数的错误值。在后一种情况下,压力扩散效应可能会出现,就像双多孔介质中一样。
超声测量方法估计:
在1996年,Leclaire 等人 [LKLBMC96]引入了一种方法,用于从超声波测量中(即在高于 20k Hz 的频率或声波波长小于约1.7毫米时)估算热特征长度Λ′和粘性特征长度Λ。Leclaire 等人描述的方法要求多孔介质的流体相依次被空气和氦饱和。通过使用这两种流体的测量结果,可以评估由于高频下粘-惯性效应引起的声能耗散(由Λ在高频下表征),以及由于当声波波长高于多孔微结构的特征尺寸时而发生的瑞利散射,而又不大于它。
2010 年,受到 Olny和Panneton 的工作启发,Groby 等人 [GORSL10]提出了一种从超声波测量中估算热特征长度、粘性特征长度、开放孔隙度和动态扭曲度的高频限制的方法,该方法使用了反射和透射系数。该方法不需要先验知识来估算静态气流阻力。然而,它不能用于估算静态热渗透率。
这些超声波方法的缺点是瑞利散射的先验未知效应。在 Groby 等人的工作中,这种效应可能导致参数的错误值。在 Leclaire 等人的工作中,瑞利散射效应可以被评估,但测量已经进行了两次(在两种不同的饱和流体中)。
参考文献:
[OPT02] Olny X., Panneton R., Tran-Van J., An indirect acoustical method for determining intrinsic parameters of porous materials in Poromechanics II, proceedings of the 2nd Biot conference, Grenoble (France), 2002. →
[OP08] Olny X., Panneton R., Acoustical determination of the parameters governing thermal dissipation in porous media, J. Acoust. Soc. Am. 123(2), 2008, pp. 814–824, →
[CA91] Champoux Y. and Allard J.-F., Dynamic tortuosity and bulk modulus in air-saturated porous media, J. Appl. Phys. 70, 1991, pp. 1975-1979 →
[LLAT97] Lafarge D., Lemarinier P., Allard J.-F. and Tarnow V., Dynamic compressibility of air in porous structures at audible frequencies, J. Acoust. Soc. Am. 102(4), 1997, pp. 1995-2006 →
[LKLBMC96] Leclaire P., Kelders L., Lauriks W. , Brown N., Melon M., Castagnède, Determination of the viscous and thermal characteristic lengths of plastic foams by ultrasonic measurements in helium and air, J. Appl. Phys. 80(4), pp. 2009–2012, 1996 →
[GORSL10] Groby J.-P, Ogam E, De Ryck L., Sebaa N., Lauriks W., Analytical method for the ultrasonic characterization of homogeneous rigid porous materials from transmitted and reflected coefficients, J. Acoust. Soc. Am. 127(2), pp. 764–772, 2010 →
静态热渗透率表征:
可以通过测量多孔介质的动态体积模量,并在了解开放孔隙度的先验知识的情况下,估算出静态热渗透率 k′0(参见[OPT02,PO06])。
[OPT02] Olny X., Panneton R., Tran-Van J., An indirect acoustical method for determining intrinsic parameters of porous materials in Poromechanics II, proceedings of the 2nd Biot conference, Grenoble (France), 2002. →
[PO06] Panneton R., Olny X., Acoustical determination of the parameters governing viscous dissipation in porous media, J. Acoust. Soc. Am. 119(4), 2006, pp. 2027–2040, →
声学参数的条件:
在声学表征过程中,可以对结果进行一些一致性检查。虽然模型中使用的所有参数都应该是独立的,但应验证一些不等式或数量级的范围。此外,对于一些特定的材料形态,参数之间可能存在一些关联。根据定义,特征粘性长度应小于或等于热特征长度:
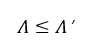
对于纤维或毡类材料,通常认为静态气流阻力随质量密度增加而增加 [Tar96]。纤维或毡类材料的扭曲度可以用以下近似表示(参见 Umnova 等人[UAM00]):

这个方程有时被称为阿奇(Archie)经验定律[Arc42]:[(1/ϕ)]^r。通过不同的推理,Tournat等人[TPLJ04]推导出了垂直于平行相同圆柱轴的声流的表达式α_∞=1+(1-ϕ)。显然,这个最后的表达式是围绕ϕ=1展开的泰勒展开,展开到α_∞≃1/ϕ的1阶。通过图形观察,可以看出对于ϕ≲ 0.96,这两个α_∞的表达式发散。
一叠相同固体球的扭曲度由J. G. Berryman[Ber80]计算如下:

此外,可以检查以下值:
基于 Johnson Koplik & Dashen 工作的模型的粘性孔形状因子M。
基于 Champoux-Allard-Lafarge 工作的模型的热孔形状因子M′。
对于通常的声学多孔材料,孔形状因子M和M′的数量级应该在1左右。对于直筒形孔,M=M′=1。
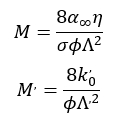
参考文献:
[Tar96] Tarnow V., Airflow resistivity of models of fibrous acoustic materials, J. Acoust. Soc. Am. 100(6), pp. 3706-3713, 1996
[UAL00] Umnova O., Attenborough K., Li K. M., A cell model for the acoustical properties of fibrous absorbents in proc. of Internoise 2000 (Nice, France), 2000
[Arc42] G. Archie, The electrical resistivity log as an aid in determining some reservoir characteristics Transactions of AIME 146, pp. 54-62, 1942
[TPLJ04] Tournat V., Pagneux V., Lafarge D., Jaouen L. Multiple scattering of acoustic waves and porous absorbing media, Phys. Rev. E 70, 026609, 2004
[Ber80] Berryman J. G., Confirmation of Biot’s theory, Appl. Phys. Lett., 37, pp. 382-384, 1980
